- Published on
- |Views: 23|37 min read
Understanding DeepSeek's Multi-Head Latent Attention (MLA)
- Authors

- Name
- Shashank Shekhar
- @sshkhr16
This is Part 1 of a three-part series on DeepSeek's FlashMLA, based on my talk at the Toronto Machine Learning Summit 2025.
- Part 1: Multi-Head Latent Attention (this post)
- Part 2: Flash Attention (coming soon)
- Part 3: FlashMLA (coming soon)
All code samples from this particular post are available in this GitHub repository: github.com/sshkhr/mla-pytorch
A Brief Recap of Multi-Head Scaled Dot Product Attention
Attention is all you need by Vaswani et al introduced the now ubiquitous transformer architecture, scaled dot-product attention, as well as the multi-head attention mechanism, which is the de facto form of attention one thinks of in transformers.

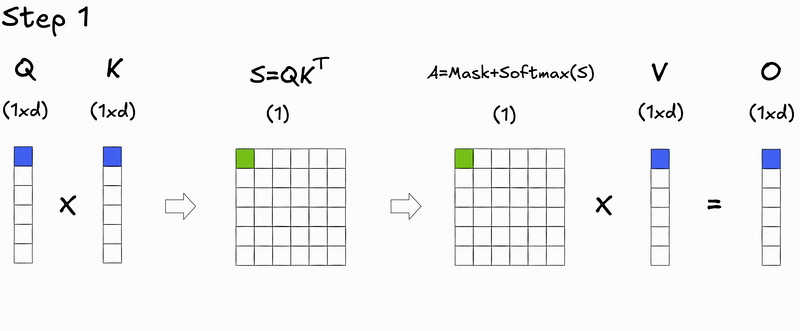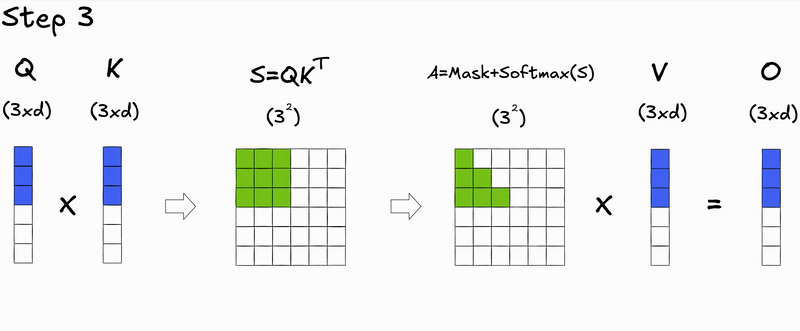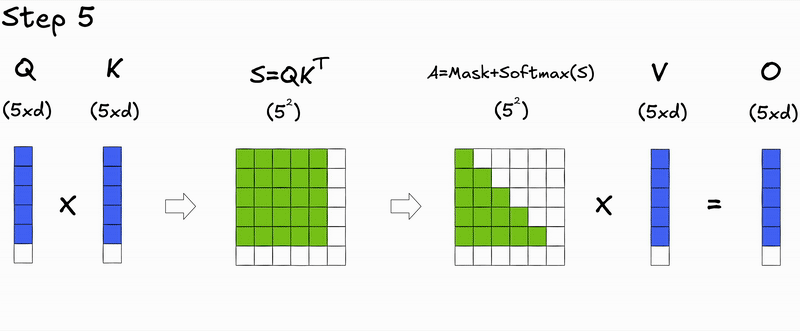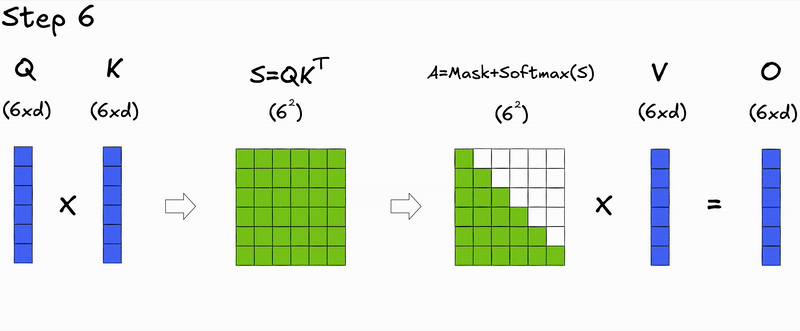
In scaled dot-product attention (SDPA), given a set of queries , keys , and values (vectors derived from input tokens), attention computes a weighted sum of the values, where each query-key pair’s weight is proportional to their similarity. A simple approach to calculating similarity between tokens is by taking a dot product of the query and key vectors. The product is then scaled by the square root of the key dimension (in order to preserve an appropriate variance in the attention). Optionally, a mask is applied e.g. to compute only scores for a token based on all previous tokens in an autoregressive setting, not the future tokens. Lastly, a softmax operation is applied to get a probability distribution over the tokens. The attention weights are then used to produce a weighted sum of the values as the output:
If you prefer code to math, here is a minimal PyTorch implementation of scaled dot-product attention (optimized for reading clarity, to match the diagram above):
import torch
import torch.nn as nn
import torch.nn.functional as F
import math
class ScaledDotProductAttention(nn.Module):
"""
Scaled Dot-Product Attention as described in "Attention Is All You Need"
"""
def __init__(self):
super().__init__()
def forward(self, Q, K, V, mask=None):
"""
Args:
Q: Query tensor of shape (batch_size, seq_len_q, d_k)
K: Key tensor of shape (batch_size, seq_len_k, d_k)
V: Value tensor of shape (batch_size, seq_len_v, d_v)
mask: Optional mask tensor of shape (batch_size, seq_len_q, seq_len_k)
Returns:
output: Attention output of shape (batch_size, seq_len_q, d_v)
attention_weights: Attention weights of shape (batch_size, seq_len_q, seq_len_k)
"""
batch_size, seq_len_q, d_k = Q.shape
seq_len_k = K.shape[1]
# Step 1: Compute raw attention scores Q @ K^T
# (batch_size, seq_len_q, d_k) @ (batch_size, d_k, seq_len_k) -> (batch_size, seq_len_q, seq_len_k)
attention_scores = torch.matmul(Q, K.transpose(-2, -1))
# Step 2: Scale by sqrt(d_k)
attention_scores = attention_scores / math.sqrt(d_k)
# Step 3: Apply mask (if provided)
if mask is not None:
attention_scores = attention_scores + mask # mask should contain -inf for masked positions
# Step 4: Apply softmax to get attention weights
attention_weights = F.softmax(attention_scores, dim=-1) # (batch_size, seq_len_q, seq_len_k)
# Step 5: Apply attention weights to values
# (batch_size, seq_len_q, seq_len_k) @ (batch_size, seq_len_k, d_v) -> (batch_size, seq_len_q, d_v)
output = torch.matmul(attention_weights, V)
return output, attention_weights
We will see more details on the exact shapes and sizes of the tensors in a bit, as this is fundamental to understanding the bottlenecks in the standard attention mechanism which necessitated MLA. But before that, we need to mention that scaled dot-product attention is usually not used in isolation. Each layer has multiple attention heads and the setup used is called multi-head attention. The different attention "heads" are simply several scaled dot-product attention modules running in parallel, each operating on a different learned projection of the input. Instead of one single attention computation with very large , we split the queries, keys, and values into (for example) 8 or 16 smaller sets (heads), perform attention in each subspace, and then concatenate the results. Here is a simple PyTorch implementation of multi-head attention that utilizes the scaled dot-product attention we defined above:
Multi-Head Attention Implementation
class MultiHeadAttention(nn.Module):
"""
Multi-Head Attention mechanism that applies multiple scaled dot-product attention heads in parallel
"""
def __init__(self, d_model, n_heads):
"""
Args:
d_model: Model dimension (embedding dimension)
n_heads: Number of attention heads
"""
super().__init__()
assert d_model % n_heads == 0, "d_model must be divisible by n_heads"
self.d_model = d_model
self.n_heads = n_heads
self.d_k = d_model // n_heads # dimension per head (d_k = d_v in standard implementation)
# Linear projection layers
self.W_q = nn.Linear(d_model, d_model, bias=False) # Query projection
self.W_k = nn.Linear(d_model, d_model, bias=False) # Key projection
self.W_v = nn.Linear(d_model, d_model, bias=False) # Value projection
self.W_o = nn.Linear(d_model, d_model, bias=False) # Output projection
# Scaled dot-product attention module
self.attention = ScaledDotProductAttention()
def forward(self, x, mask=None):
"""
Args:
x: Input tensor of shape (batch_size, seq_len, d_model)
mask: Optional mask tensor of shape (batch_size, seq_len, seq_len)
Returns:
output: Multi-head attention output of shape (batch_size, seq_len, d_model)
"""
batch_size, seq_len, d_model = x.shape
# Step 1: Linear projections for Q, K, V
# Each projection: (batch_size, seq_len, d_model) -> (batch_size, seq_len, d_model)
Q = self.W_q(x) # (batch_size, seq_len, d_model)
K = self.W_k(x) # (batch_size, seq_len, d_model)
V = self.W_v(x) # (batch_size, seq_len, d_model)
# Step 2: Reshape and split into multiple heads
# (batch_size, seq_len, d_model) -> (batch_size, seq_len, n_heads, d_k) -> (batch_size, n_heads, seq_len, d_k)
Q = Q.view(batch_size, seq_len, self.n_heads, self.d_k).transpose(1, 2)
K = K.view(batch_size, seq_len, self.n_heads, self.d_k).transpose(1, 2)
V = V.view(batch_size, seq_len, self.n_heads, self.d_k).transpose(1, 2)
# Step 3: Apply scaled dot-product attention to each head
# Reshape to apply attention: (batch_size * n_heads, seq_len, d_k)
Q_reshaped = Q.contiguous().view(batch_size * self.n_heads, seq_len, self.d_k)
K_reshaped = K.contiguous().view(batch_size * self.n_heads, seq_len, self.d_k)
V_reshaped = V.contiguous().view(batch_size * self.n_heads, seq_len, self.d_k)
# Apply mask to all heads if provided
if mask is not None:
# Expand mask for all heads: (batch_size, seq_len, seq_len) -> (batch_size * n_heads, seq_len, seq_len)
mask_expanded = mask.unsqueeze(1).repeat(1, self.n_heads, 1, 1).view(batch_size * self.n_heads, seq_len, seq_len)
else:
mask_expanded = None
# Apply attention: (batch_size * n_heads, seq_len, d_k)
attention_output, _ = self.attention(Q_reshaped, K_reshaped, V_reshaped, mask_expanded)
# Step 4: Concatenate heads
# (batch_size * n_heads, seq_len, d_k) -> (batch_size, n_heads, seq_len, d_k) -> (batch_size, seq_len, d_model)
attention_output = attention_output.view(batch_size, self.n_heads, seq_len, self.d_k)
attention_output = attention_output.transpose(1, 2).contiguous().view(batch_size, seq_len, d_model)
# Step 5: Final linear projection
output = self.W_o(attention_output) # (batch_size, seq_len, d_model)
return output
Multi-head attention allows the model to focus on different positions or features in different heads. For example, one head might attend strongly to very nearby tokens while another attends to tokens far back, etc. The output of MHA is the same shape as the input (d_model), so it can be added back to the input (residual connection) and fed into the next layer.
Why Attention Scales with Sequence Length
Now that we have the MHA machinery in place, let's examine where the computational bottleneck arises. The culprit is the attention score computation:
Consider the shapes involved (per batch, per head):
The matrix multiplication requires computing dot products, each of dimension . That's operations per head, per layer. Since is typically fixed (64-256), the dominant term is the quadratic dependence on sequence length.

Let's make this concrete with some numbers:
import torch
def attention_tensor_sizes(batch_size, seq_len, d_model, n_heads, dtype=torch.float16):
"""Calculate tensor sizes for MHA computation."""
d_h = d_model // n_heads
bytes_per_elem = torch.tensor([], dtype=dtype).element_size()
# Per-head shapes
Q_shape = (batch_size, n_heads, seq_len, d_h)
K_shape = (batch_size, n_heads, seq_len, d_h)
V_shape = (batch_size, n_heads, seq_len, d_h)
attn_scores_shape = (batch_size, n_heads, seq_len, seq_len) # The N×N matrix
# Memory in bytes
qkv_memory = 3 * batch_size * n_heads * seq_len * d_h * bytes_per_elem
attn_matrix_memory = batch_size * n_heads * seq_len * seq_len * bytes_per_elem
return {
"Q/K/V each": Q_shape,
"Attention scores": attn_scores_shape,
"QKV memory (MB)": qkv_memory / (1024**2),
"Attention matrix memory (MB)": attn_matrix_memory / (1024**2),
}
Let's compare what the attention matrix memory looks like as we scale up sequence length for GPT-2 (=768, 12 heads) and DeepSeek-V2 (=5120, 128 heads):
| Sequence Length | GPT-2 Attention | DeepSeek-V2 Attention |
|---|---|---|
| 512 | 6 MB | 64 MB |
| 1024 | 24 MB | 256 MB |
| 2048 | 96 MB | 1.0 GB |
| 4096 | 384 MB | 4.0 GB |
| 8192 | 1.5 GB | 16.0 GB |
| 16384 | 6.0 GB | 64.0 GB |
| 32768 | 24.0 GB | 256.0 GB |
| 65536 | 96.0 GB | 1,024.0 GB |
The quadratic scaling is brutal. At DeepSeek-V2 scale with 64K context, the attention matrix alone requires 1 TB of memory—per layer, per forward pass. This is clearly untenable.

KV Caching: Trading Memory for Compute
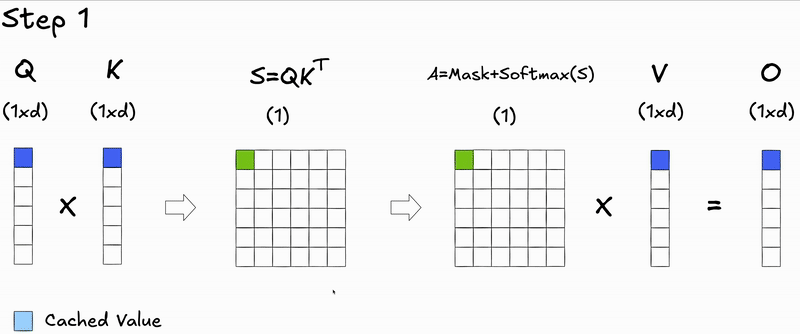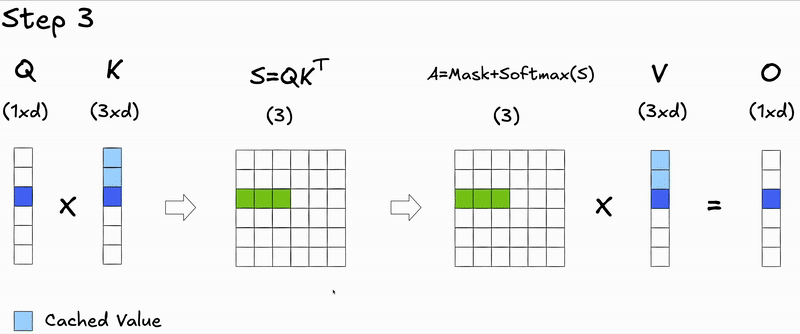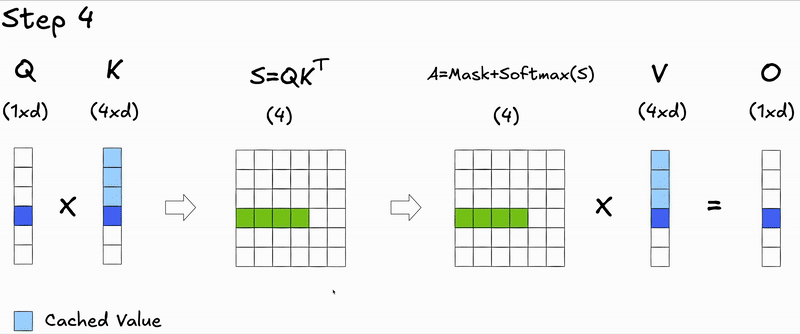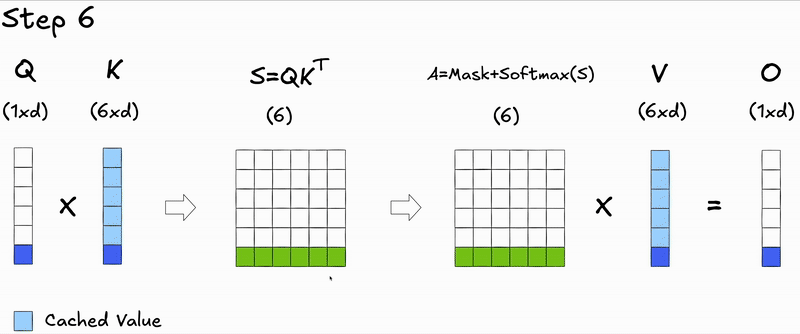
Let's take a closer look at the matrix operations during the token generation process at inference time for the autoregressive transformer:
Notice anything interesting 👀? Not yet?
How about if we focus on the step-by-step decoding process?
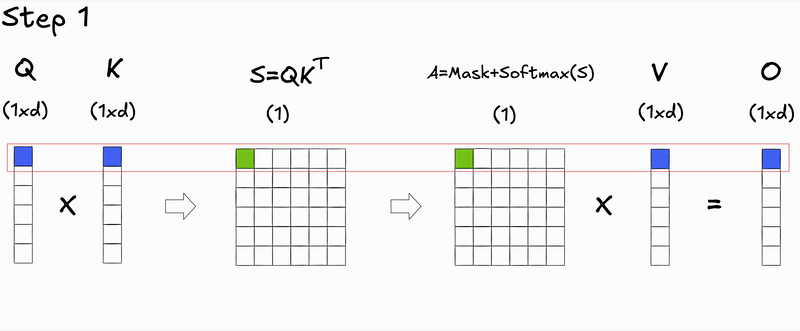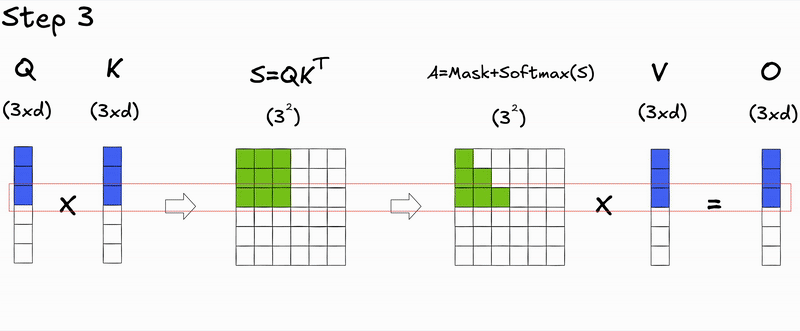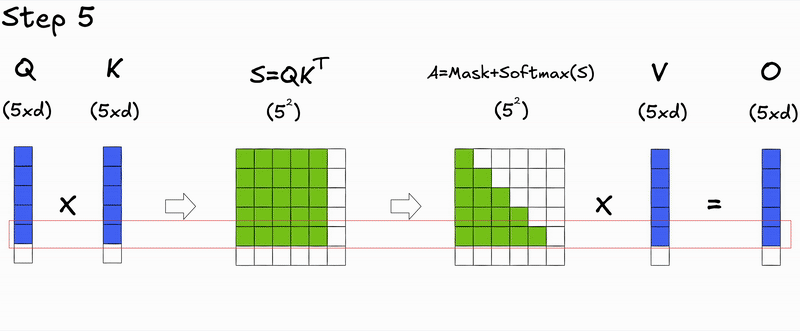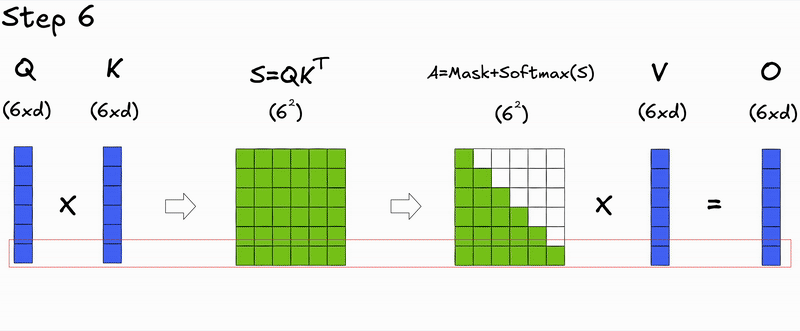
Here's a key insight: during autoregressive generation, we decode one token at a time. At step , we only need to compute attention for the new query against all previous keys and values. The attention scores for previous tokens don't change—we're just appending a new row.
During prefill (processing the initial input context), we compute attention for all tokens simultaneously, resulting in the full attention matrix.
During decoding (generating new tokens), we only compute attention for the new token's query against all previous keys and values, resulting in a single row of the attention matrix.
This observation leads us to KV caching: instead of recomputing and for all previous generated tokens at each step during inference, we cache them and only compute the projections for the new token:
We cache and because the keys and values for previous tokens remain unchanged - only the new token's query needs to attend to them.
Here's a PyTorch implementation that makes the caching logic concrete:
class MultiHeadAttentionWithKVCache(nn.Module):
def __init__(self, d_model, n_heads, max_seq_len=4096):
super().__init__()
self.d_model = d_model
self.n_heads = n_heads
self.d_h = d_model // n_heads
self.W_q = nn.Linear(d_model, d_model, bias=False)
self.W_k = nn.Linear(d_model, d_model, bias=False)
self.W_v = nn.Linear(d_model, d_model, bias=False)
self.W_o = nn.Linear(d_model, d_model, bias=False)
# Pre-allocated KV cache buffers (no allocation during decode)
self.register_buffer('k_cache', torch.zeros(1, n_heads, max_seq_len, self.d_h))
self.register_buffer('v_cache', torch.zeros(1, n_heads, max_seq_len, self.d_h))
self.cache_position = 0
def forward(self, x, use_cache=False):
"""
Args:
x: Input tensor. During prefill: (B, N, d_model). During decode: (B, 1, d_model)
use_cache: Whether to use/update the KV cache
"""
B, seq_len, _ = x.shape
# Compute Q, K, V for current input
Q = self.W_q(x).view(B, seq_len, self.n_heads, self.d_h).transpose(1, 2)
K = self.W_k(x).view(B, seq_len, self.n_heads, self.d_h).transpose(1, 2)
V = self.W_v(x).view(B, seq_len, self.n_heads, self.d_h).transpose(1, 2)
if use_cache:
# Write to pre-allocated buffer (no new allocation)
start = self.cache_position
end = start + seq_len
self.k_cache[:B, :, start:end, :] = K
self.v_cache[:B, :, start:end, :] = V
self.cache_position = end
# Attend over full cached sequence
K = self.k_cache[:B, :, :end, :]
V = self.v_cache[:B, :, :end, :]
# Standard attention computation
# Q: (B, n_heads, seq_len, d_h) - seq_len=1 during decode
# K: (B, n_heads, cache_len, d_h)
scores = torch.matmul(Q, K.transpose(-2, -1)) / math.sqrt(self.d_h)
attn_weights = F.softmax(scores, dim=-1)
output = torch.matmul(attn_weights, V)
# Reshape and project
output = output.transpose(1, 2).contiguous().view(B, seq_len, self.d_model)
return self.W_o(output)
def reset_cache(self):
self.k_cache.zero_()
self.v_cache.zero_()
self.cache_position = 0
The complexity tradeoff is stark:
| Without KV Cache | With KV Cache | |
|---|---|---|
| compute per step | ||
| Memory per step |
We've converted a compute-bound problem into a memory-bound one... but how memory-bound? Let's quantify it.
The KV Cache Memory Wall
How much memory does the KV cache actually require? Each decoding step now requires only operations (the new query attending to cached keys), but we need to store all those keys and values. Let's work through the math for a small model (GPT-2):
def measure_kv_cache_memory(d_model, n_heads, seq_len, dtype=torch.float16):
"""Calculate KV cache memory in MB."""
d_h = d_model // n_heads
bytes_per_elem = torch.tensor([], dtype=dtype).element_size()
kv_cache_bytes = 2 * n_heads * seq_len * d_h * bytes_per_elem
return kv_cache_bytes / (1024**2)
| Tokens | With Cache (s) | No Cache (s) | Speedup | Cache (MB) |
|---|---|---|---|---|
| 128 | 0.0293 | 0.0298 | 1.0x | 0.4 |
| 256 | 0.0585 | 0.0599 | 1.0x | 0.8 |
| 512 | 0.1176 | 0.1543 | 1.3x | 1.5 |
| 1024 | 0.2351 | 0.6065 | 2.6x | 3.0 |
| 2048 | 0.4851 | 3.5300 | 7.3x | 6.0 |
| 4096 | 0.9691 | 24.4924 | 25.3x | 12.0 |
On an NVIDIA 5060 Ti, decoding with a context window of 4096 tokens:
- KV caching provides a 25.3x speedup
- At the cost of 12.0 MB of cache memory

At GPT-2 scale (768 dim, 12 heads), 12 MB for 4K tokens seems manageable. But GPT-2 is a relic by modern standards—its 1.5B parameters and 1024-token context window are dwarfed by today's frontier models. The field has moved aggressively toward longer contexts, and for good reason.
Side Note: Why Long Context Matters
The push toward longer context windows isn't just about bragging rights. Several concrete capabilities unlock as context grows
In-context learning improves with more examples. The landmark GPT-3 paper (Brown et al., 2020) demonstrated that few-shot performance scales with the number of demonstrations. More context means more examples, which means better task adaptation without fine-tuning. Recent work on many-shot in-context learning (Agarwal et al., 2024) shows this scaling continues well into hundreds or thousands of examples—if you have the context window to fit them.
Complex reasoning requires extended working memory. Chain-of-thought prompting (Wei et al., 2022) and its descendants rely on the model "thinking out loud" across many tokens. For difficult problems—multi-step mathematics, code debugging, legal analysis—the reasoning trace itself can consume tens of thousands of tokens. Models like OpenAI's o1 and DeepSeek-R1 (DeepSeek-AI, 2025) generate extensive internal reasoning chains that would be impossible with short contexts.
Agentic workflows are inherently multi-turn. When LLMs operate as agents—browsing the web, writing and executing code, interacting with APIs—the conversation history accumulates rapidly. A single agentic session with tool calls, observations, and corrections can easily span 50K+ tokens. Projects like AutoGPT, OpenDevin, and Claude's computer use all stress-test context limits.
Vision Transformers process images as sequences of patches—a single 1024×1024 image at 16×16 patch size yields 4,096 tokens. Video understanding multiplies this by frame count. Gemini 1.5 demonstrated 1M+ token contexts partly to handle hour-long videos. Robotics applications processing continuous sensor streams face similar challenges.
Now that we know why we care about long context inference, let's now consider what KV caching looks like at the scale of a modern frontier model. DeepSeek-V2 (DeepSeek-AI, 2024) uses 60 attention layers with 128 heads per layer and a head dimension of 128. The model supports 128K token contexts.
For standard multi-head attention, the KV cache per token requires storing and vectors for every head in every layer:
DeepSeek-V2 KV Cache (hypothetical standard MHA) with 60 layers, 128 heads, d_h=128, fp16:
| Context Length | KV Cache Memory |
|---|---|
| 1K tokens | 3.7 GB |
| 4K tokens | 14.6 GB |
| 32K tokens | 117.2 GB |
| 128K tokens | 468.8 GB |
At 128K context, the KV cache alone would require ~470 GB—far exceeding even the largest single GPU (H100 has 80GB). This is a fundamental blocker for long-context inference.
The situation compounds when we consider production realities of inference:
- Batch size > 1: KV cache scales linearly with batch size. Serving 8 concurrent requests at 32K context would require nearly 1 TB just for the cache.
- Multiple users: Production systems serve thousands of concurrent sessions. Even with sophisticated memory management (paging, offloading), the aggregate memory pressure is immense.
- Model weights: The parameters themselves still need ~30-60GB in fp16. The KV cache competes for the same limited HBM.
We've traded one impossible problem (quadratic compute) for another (linear but massive memory). The field has developed several approaches to address this memory wall. Each makes different tradeoffs between memory efficiency and model capacity. Let's examine them.
Attention Variants
The memory wall has motivated several architectural modifications that reduce KV cache size by sharing key-value heads across multiple query heads.

Multi-Query Attention (MQA) (Shazeer, 2019) was the first major attempt to address KV cache bloat. The idea is simple: instead of each attention head having its own and projections, all heads share a single and a single . The queries remain independent (hence "multi-query"), but the keys and values are computed once and broadcast to all heads.
Grouped-Query Attention (GQA) (Ainslie et al., 2023) is a middle ground. Instead of all heads sharing one KV pair (MQA) or each head having its own (MHA), GQA divides the query heads into groups, where each group shares a single KV pair. This interpolates between MHA () and MQA ().
You can compare the three attention variants using their minimal implementations below:
 KV cache memory usage comparison for Multi-Head Attention (MHA), Grouped-Query Attention (GQA), and Multi-Query Attention (MQA) for 1 layer at DeepSeek-V2 scale (128 heads, head dim 128, fp16).
KV cache memory usage comparison for Multi-Head Attention (MHA), Grouped-Query Attention (GQA), and Multi-Query Attention (MQA) for 1 layer at DeepSeek-V2 scale (128 heads, head dim 128, fp16).The memory savings are substantial. We show the savings per layer in the figure above. But the real benefit comes when we scale to full models and long contexts. Over a full 128K token context at DeepSeek-V2 scale, the KV cache sizes are:
| Multi-Head (MHA) | Grouped-Query (GQA) | Multi-Query (MQA) | |
|---|---|---|---|
| KV cache per token | |||
| KV cache size per token | 4 MB | 500 KB | 31 KB |
| KV cache for 128K context | 512 GB | 64 GB | ~4 GB |
| Model quality | High | Medium | Low |
where:
- = number of query heads
- = number of KV head groups (GQA parameter)
- = dimension per head
- = number of layers
MQA reduces the 128K cache from 512 GB to just 4 GB! But the savings in memory come at the cost of reduced model capacity.
The Capacity Tradeoff
The multiple heads in MHA aren't just redundancy. Each head (in theory) learns to attend to different aspects of the input—one head might track syntactic dependencies, another semantic similarity, another positional relationships. When we force all heads to share the same keys and values, we're compressing this representational diversity.
Empirically, MQA degrades model quality. The original MQA paper showed modest perplexity increases, but subsequent work found larger gaps on downstream tasks, particularly for complex reasoning. GQA recovers much of the quality while retaining most of the memory savings, which is why models like Llama 2 70B and Mistral adopted it.
But we're still making a tradeoff: memory efficiency versus representational capacity. What if we could have both?
Multi-Head Latent Attention : Low-Rank Decomposition of KV matrices
GQA and MQA reduce cache size by sharing KV heads, but they sacrifice model capacity in the process. Deepseek's Multi-Head Latent Attention takes a fundamentally different approach: instead of sharing heads, it compresses the KV representations into a low-dimensional latent space.
Let's take a look again at standard multi-head attention.

The KV cache stores the projected keys and values for each token:
where is the input sequence and are the projection matrices. The cache stores and , which have dimension per token.
But here's the question: do we really need to store the full projected representations?
The KV projections map from -dimensional inputs to -dimensional outputs. For DeepSeek-V2, that's mapping from 5120 dimensions to dimensions. What if the "useful" information in those 16K dimensions actually lives in a much smaller subspace?
This idea—that high-dimensional representations can be approximated by low-dimensional ones—is a recurring theme in machine learning:
The principle of low-rank factorization appears throughout ML:
- LoRA (Hu et al., 2021): Fine-tunes large models by learning low-rank updates where and with
- Bottleneck layers: ResNet and Inception use 1×1 convolutions to compress channels before expensive 3×3 operations
- Autoencoders: Compress inputs to a latent space, then reconstruct—the latent captures the "essential" information
- Matrix factorization: Recommendation systems approximate user-item matrices as products of low-rank factors
The common insight: real-world data often has intrinsic dimensionality much lower than its ambient dimensionality.
For a weight matrix , we can approximate it as:
where and , with compression dimension .

The intermediate representation after lives in a compressed -dimensional space. If we're strategic about what we cache, we can store this compressed representation instead of the full projection.
Multi-Head Latent Attention applies this principle directly to the KV projections. Instead of:
MLA first projects to a shared low-dimensional latent representation, then expands back:
where:
- projects to the compressed latent space
- expands latent to keys
- expands latent to values
- is the latent/compression dimension (e.g., 512 in DeepSeek-V2)
The crucial insight: we only need to cache , not the full and . The up-projections and are static weights—we can apply them on-the-fly during attention computation.

The cache size per token drops from (for K and V) to just . For DeepSeek-V2 with , , and :
For DeepSeek-V2's parameters, this is a 64X reduction in KV cache size—comparable to MQA's savings, but without sacrificing the representational capacity of having many independent heads.
Here's the implementation:
Query Compression and RoPE in MLA
The implementation above uses a standard query projection (W_q) for simplicity. However, DeepSeek-V2/V3 also compress the queries via a low-rank decomposition, mirroring the KV compression:
where down-projects to a query latent, RMSNorm normalizes it, and up-projects back to full query dimension. DeepSeek-V2 uses .
Unlike the KV latent, the query latent is not cached — it's only needed for the current token. The purpose is parameter efficiency: the two smaller matrices and have fewer total parameters than a single full-rank .
The RoPE embedding is also operated on separately to preserve the positional embeddings, since standard low-rank projection would mix positional and content information.
This is the full architecture of MLA with query compression and RoPE (taken from the DeepSeek-V3 paper):

Here is the full MLA implementation with query compression. We will skip the RoPE details for now, as they are not important for understanding the core idea of latent KV compression:
class RMSNorm(nn.Module):
"""Root Mean Square Layer Normalization."""
def __init__(self, dim, eps=1e-6):
super().__init__()
self.eps = eps
self.weight = nn.Parameter(torch.ones(dim))
def forward(self, x):
rms = torch.sqrt(torch.mean(x ** 2, dim=-1, keepdim=True) + self.eps)
return x / rms * self.weight
class MultiHeadLatentAttention(nn.Module):
"""
MLA with both query and KV compression.
Query: x -> W_dq -> RMSNorm -> W_uq -> Q (not cached)
KV: x -> W_dkv -> L_kv (cached) -> W_uk/W_uv -> K, V
"""
def __init__(self, d_model, n_heads, d_c, d_cq, max_seq_len=4096):
super().__init__()
self.n_heads = n_heads
self.d_h = d_model // n_heads
self.d_c = d_c
self.d_cq = d_cq
# Query compression: down-project, normalize, up-project
self.W_dq = nn.Linear(d_model, d_cq, bias=False)
self.q_norm = RMSNorm(d_cq)
self.W_uq = nn.Linear(d_cq, n_heads * self.d_h, bias=False)
# KV compression
self.W_dkv = nn.Linear(d_model, d_c, bias=False)
self.W_uk = nn.Linear(d_c, n_heads * self.d_h, bias=False)
self.W_uv = nn.Linear(d_c, n_heads * self.d_h, bias=False)
self.W_o = nn.Linear(n_heads * self.d_h, d_model, bias=False)
# Pre-allocated latent cache
self.register_buffer('latent_cache', torch.zeros(1, max_seq_len, d_c))
self.cache_position = 0
def forward(self, x, use_cache=False):
B, N, _ = x.shape
# Query: down-project -> normalize -> up-project
L_q = self.q_norm(self.W_dq(x))
Q = self.W_uq(L_q).view(B, N, self.n_heads, self.d_h).transpose(1, 2)
# KV: compress to latent
L_kv = self.W_dkv(x)
if use_cache:
start = self.cache_position
end = start + N
self.latent_cache[:B, start:end, :] = L_kv
self.cache_position = end
L_kv = self.latent_cache[:B, :end, :]
# Expand latent to full K, V (on-the-fly, not cached)
K = self.W_uk(L_kv).view(B, -1, self.n_heads, self.d_h).transpose(1, 2)
V = self.W_uv(L_kv).view(B, -1, self.n_heads, self.d_h).transpose(1, 2)
scores = torch.matmul(Q, K.transpose(-2, -1)) / math.sqrt(self.d_h)
attn = F.softmax(scores, dim=-1)
out = torch.matmul(attn, V)
out = out.transpose(1, 2).contiguous().view(B, N, -1)
return self.W_o(out)
def cache_size_per_token(self):
return self.d_c # Query compression doesn't affect cache size
Note that query compression does not affect cache size — only the KV latent is cached. With the absorption trick (below), the absorbed query projection becomes , applied after the query compression and normalization.
The Absorption Trick: Making MLA Hardware-Friendly
The naive MLA implementation above has a problem: during decoding, we need to expand the entire cached latent sequence through and at every step. For a 100K token context, that's a lot of extra compute.
But there's a clever mathematical trick that eliminates this overhead. Let's trace through the attention computation:
We can absorb into the query projection by defining:
Now the attention scores become:
The queries are projected directly into the latent space, and we compute attention against the cached latents without ever materializing the full keys!
Similarly, for the value side, instead of computing and then applying , we can absorb into the output projection:
The full absorbed computation becomes:

This is remarkable: the attention operation itself is unchanged—it's still followed by softmax and multiplication with values. We've just redefined what , , and mean. The latent plays the role of both keys and values!
The absorbed version has a crucial advantage: attention is computed entirely in the latent space. We never materialize the full -dimensional keys and values. This means:
- Memory: Cache remains at per token (same as naive MLA)
- Compute: No per-step expansion of cached latents through ,
- Hardware compatibility: The attention pattern () is identical to standard attention
That last point is critical. Because the absorbed MLA has the same computational structure as standard attention, we can leverage highly optimized attention kernels like FlashAttention. The latent simply plays the role of a compressed key/value representation.
In the next post, we'll explore how FlashAttention's memory-efficient tiling strategy applies directly to MLA's latent attention. The absorption trick isn't just mathematically elegant—it's the key to achieving both memory efficiency and computational efficiency on modern GPUs.
Summary
Let's compare the cache sizes across all the approaches we've covered:
| MHA | GQA () | MQA | MLA () | |
|---|---|---|---|---|
| KV cache per token | ||||
| Cache size (DeepSeek-V2) | 3.9 MB | 244 KB | 15 KB | 60 KB |
| 128K context | 512 GB | 32 GB | 2 GB | 8 GB |
| Relative to MHA | 1× | 16× | 256× | 64× |
| Model quality | Baseline | Slight degradation | Significant degradation | Matches baseline |
MLA achieves compression comparable to MQA while maintaining the representational capacity of full MHA. The key insight is that compression happens in a learned latent space, not by arbitrarily sharing heads.
The DeepSeek team reports that MLA matches or exceeds MHA performance on their benchmarks while reducing KV cache by ~57X. This is the breakthrough that makes 128K+ context windows practical on commodity hardware.
References
[1] Shazeer, N. (2019). Fast Transformer Decoding: One Write-Head is All You Need. arXiv preprint arXiv:1911.02150. — Introduced Multi-Query Attention (MQA).
[2] Ainslie, J., Lee-Thorp, J., de Jong, M., Zemlyanskiy, Y., Lebrón, F., & Sanghai, S. (2023). GQA: Training Generalized Multi-Query Transformer Models from Multi-Head Checkpoints. arXiv preprint arXiv:2305.13245. — Introduced Grouped-Query Attention (GQA).
[3] DeepSeek-AI. (2024). DeepSeek-V2: A Strong, Economical, and Efficient Mixture-of-Experts Language Model. arXiv preprint arXiv:2405.04434. — Introduced Multi-Head Latent Attention (MLA).
[4] Brown, T. B., Mann, B., Ryder, N., Subbiah, M., Kaplan, J., Dhariwal, P., ... & Amodei, D. (2020). Language Models are Few-Shot Learners. Advances in Neural Information Processing Systems, 33, 1877-1901. — GPT-3 and few-shot in-context learning.
[5] Agarwal, R., Henaff, M., Kakade, S., & Sun, W. (2024). Many-Shot In-Context Learning. arXiv preprint arXiv:2404.11018. — Scaling in-context learning to hundreds/thousands of examples.
[6] Wei, J., Wang, X., Schuurmans, D., Bosma, M., Ichter, B., Xia, F., ... & Zhou, D. (2022). Chain-of-Thought Prompting Elicits Reasoning in Large Language Models. Advances in Neural Information Processing Systems, 35, 24824-24837. — Chain-of-thought prompting.
[7] DeepSeek-AI. (2025). DeepSeek-R1: Incentivizing Reasoning Capability in LLMs via Reinforcement Learning. arXiv preprint arXiv:2501.12948. — Extended reasoning traces in LLMs.
[8] Reid, M., Savinov, N., Teber, D., ... & Kavukcuoglu, K. (2024). Gemini 1.5: Unlocking Multimodal Understanding Across Millions of Tokens of Context. arXiv preprint arXiv:2403.05530. — Million-token context windows for multimodal understanding.
[9] Hu, E. J., Shen, Y., Wallis, P., Allen-Zhu, Z., Li, Y., Wang, S., ... & Chen, W. (2021). LoRA: Low-Rank Adaptation of Large Language Models. arXiv preprint arXiv:2106.09685. — Low-rank adaptation for efficient fine-tuning.
Citation
If you found this post helpful, please consider citing it:
@article{shekhar2026mla,
title = {Understanding DeepSeek's Multi-Head Latent Attention (MLA)},
author = {Shekhar, Shashank},
journal = {shashankshekhar.com},
year = {2026},
month = {February},
url = {https://shashankshekhar.com/blog/flashmla/flashmla-1-mla}
}